摘要:葛立恒数的平方是否大于原数,这个问题涉及到巨大的数值比较。葛立恒数是一个极其庞大的数,其平方意味着每个位数都要与自己相乘,结果将是一个更为巨大的数。但目前无法确定其平方是否远远大于原数,因为这需要具体的数值计算或证明,远远超出常规数学范畴。
本文目录导读:
当我们谈及数学中的大数,葛立恒数无疑是一个令人惊叹的标志性数字,当我们探讨葛立恒数的平方与其本身数值的关系时,我们不禁要思考:葛立恒数的平方是否远远大于葛立恒数本身?本文将围绕这一问题展开讨论,并尝试通过逻辑推理给出答案。
了解葛立恒数
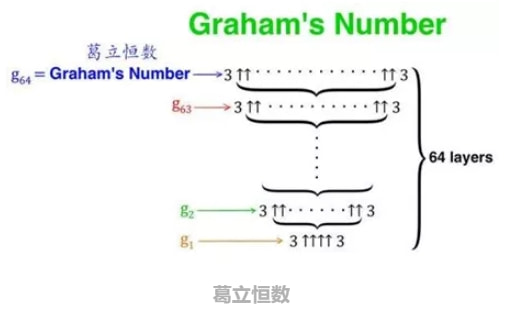
我们需要了解葛立恒数的定义及其背景,葛立恒数是由计算机科学家及数学家罗伯特·葛立恒提出的,它是一个极其庞大的数,远远超出了我们日常生活中的直观感受,葛立恒数的定义涉及到庞大的指数运算和庞大的阶乘运算,其数值之大令人难以置信。
平方数的概念
在讨论葛立恒数的平方是否远远大于葛立恒数之前,我们需要理解平方数的概念,在数学中,一个数的平方是指该数乘以自身的结果,一个数的平方可能是其原始数值的几倍甚至几十倍,当我们讨论一个非常大的数的平方时,结果可能会是一个极其庞大的数值。
逻辑推理与数学分析
我们将结合逻辑推理和数学分析来探讨这一问题,假设我们有一个非常大的数N(在这个情况下,N代表葛立恒数),那么N的平方就是N乘以N的结果,由于葛立恒数本身就是一个非常大的数,因此其平方将会是一个极其庞大的数值,从数学的角度来看,一个数的平方通常都会远大于其原始数值,我们可以推断,葛立恒数的平方确实远远大于葛立恒数本身。
对比与可视化
为了更好地理解这一观点,我们可以尝试通过对比和可视化的方法来解释,以日常生活中的例子来说明:假设我们有一个巨大的山脉,其高度已经远远超出了我们的想象,如果我们考虑这个山脉的底部到顶部的距离(即山的平方),那么这个距离无疑会远大于仅仅考虑山的高度(即山的原始数值),同样地,葛立恒数的平方也可以被看作是数学中的“山脉”,其高度(即葛立恒数)已经极其庞大,而其底部到顶部的距离(即葛立恒数的平方)更是无法想象的大。
通过了解葛立恒数的定义、平方数的概念以及逻辑推理和数学分析的方法,我们可以得出结论:葛立恒数的平方确实远远大于葛立恒数本身,这一结论在数学上具有普遍适用性,因为任何数的平方都会大于其原始数值,而葛立恒数作为一个极其庞大的数,其平方的庞大程度更是超乎我们的想象,我们可以说,葛立恒数的平方是一个远大于葛立恒数的数值,这一观点不仅为我们提供了对数学的深入理解,还展示了数学中的无穷大和无限增长的概念,通过探讨这一问题,我们可以更好地欣赏数学的魅力和无限可能性。

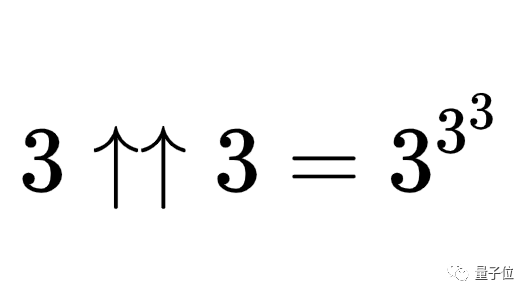

 粤ICP备19126298号
粤ICP备19126298号