摘要：微分符号是数学中的重要概念，其中dx和dy表示微小的变化量。微分符号的深层含义表示函数在某一点上的瞬时变化率或变化趋势。dx和dy则用于描述函数在自变量微小变化时的变化量，有助于计算函数的导数和切线斜率等。理解微分符号及其深层含义对于掌握微积分和数学分析的基础概念至关重要。

本文目录导读：

1. 微分符号
2. dx与dy
3. 微分符号、dx和dy的实际应用

当我们谈论微积分时，不可避免地会涉及到一些基础而重要的概念，其中微分符号、dx和dy便是核心组成部分，这些概念为理解现实世界中的连续变化和无穷小的分析提供了基础工具，本文将深入探讨微分符号、dx和dy的含义，揭示它们在数学和现实世界中的应用。

微分符号

微分是微积分中的一个基本概念，用于研究函数在某一点附近的局部行为，微分符号通常表示为"d"，用于表示一个变量相对于另一个变量的微小变化，这种变化可以是时间、距离、位置等任何连续变化的量，微分符号本身代表了无穷小的变化量，是微积分学中不可或缺的一部分。

dx与dy

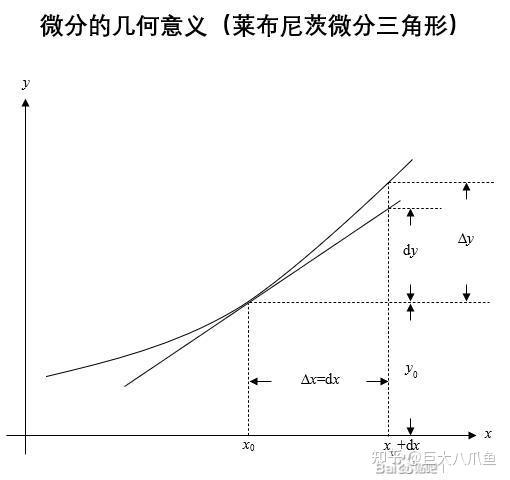
在微分中，dx和dy代表了函数自变量的微小变化量和因变量的微小变化量，假设有一个函数y = f(x)，那么dy就表示函数y在x点处的微小变化量，同样，dx表示自变量x的微小变化，这两个概念在求导过程中起着至关重要的作用。

导数定义为函数在某一点上的切线斜率，它表示函数值随自变量变化的速率，导数可以通过dy与dx的比值来求得，即f'(x) = dy/dx，这个比值表示了函数值随自变量变化的速率，或者说函数在某一点上的切线斜率。

微分符号、dx和dy的实际应用

1、物理学：在物理学中，微分符号、dx和dy被广泛应用于描述物体的运动规律，速度、加速度等物理量都可以通过导数的概念来定义，而这些物理量的变化也可以通过微分来研究。

2、经济学：在经济学中，微积分被用于分析成本、收益和利润等问题，通过对这些函数进行微分，可以找出最大化或最小化利润的点，从而帮助企业做出更好的决策。

3、生物学：生物学中的许多现象，如种群增长、药物代谢等，都可以通过微分方程来描述，微分符号、dx和dy在这里被用来描述生物系统的动态变化。

4、工程学：在工程中，微分被广泛应用于优化问题，工程师可以通过求解函数的极值（最大值或最小值）来找到最优设计方案，这些极值问题往往涉及到求导数（dy/dx），从而找到函数的拐点。

5、计算机科学：在计算机图形学和计算机动画中，微分被用来计算曲线的斜率，以便更准确地绘制图形，机器学习中的许多算法也涉及到微分，如梯度下降法等优化算法。

微分符号、dx和dy是微积分中的基础概念，它们在数学、物理、经济学、生物学和工程学等领域有着广泛的应用，通过理解这些概念，我们可以更好地研究现实世界中的连续变化和无穷小的分析，在实际应用中，我们可以通过求解导数（dy/dx）来找到函数的拐点、极值点等关键信息，从而帮助我们在各个领域做出更好的决策。

随着科技的进步和学科的发展，微分的应用将越来越广泛，为了更好地适应未来的挑战，我们需要深入理解微分的基本概念，掌握微分的求解方法，并将其应用于实际问题的解决中，只有这样，我们才能在各个领域中取得更好的成绩，为人类的进步做出贡献。

通过本文的阐述，我们了解到微分符号、dx和dy的含义及其在各个领域的应用，希望读者能够通过本文的学习，更好地掌握微分的基础知识，为未来的学习和工作打下坚实的基础。